|
Would You Rather Listen to the Lesson?
|
In precalculus, students learn about matrices and how to apply mathematical operations to them. Matrices have many useful applications, such as representing numerical data in a more compact form in tables, making it easier to manipulate it and find solutions to problems.
Regardless of their usefulness, matrices and matrix operations can come across as confusing for many students. The long lines of addition, subtraction, and multiplication can baffle even the best of students!
If you’re looking for ways to help out your students with matrices, look no further. Today, we bring you a few guidelines that will help make your matrix operations lesson as engaging as it gets!
What Are Matrices and Matrix Operations?
You can start by defining what matrices and matrix operations are. Explain that a matrix is a set of numbers in rows and columns, thus forming a rectangular arrangement by using brackets. Demonstrate what a matrix looks like, for example:
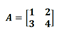
Point out that we refer to the numbers in a matrix as entries of a matrix, whereas the number of rows and columns in a matrix are called dimensions of a matrix.
You can illustrate these two with examples, for instance, in the previous matrix A, the entries are 1, 2, 3, and 4, whereas the dimensions are 2 x 2 (two rows and two columns). So it’s a 2 x 2 matrix.
Then, explain that matrix operations are simply operations with matrices, such as matrix addition, matrix subtraction, scalar multiplication, matrix multiplication, etc. By using these basic operations, we can modify matrices.

How to Do Matrix Operations
Matrix Addition and Subtraction
Explain that matrix addition means adding the numbers in the corresponding positions, whereas subtracting matrices entails subtracting the numbers in the corresponding positions. Illustrate this with a few examples, starting with addition.
For instance, you can use the following two matrices and show students how to add them:
![]()
![]()
A + B = ?
By adding the entries in the matching positions, we’ll get:
8 + 2 = 10 4 + (-6) = -2
3 + (-7) = – 4 0 + 2 = 2
Now we’ll simply write the four sums in the corresponding order in brackets, that is:
![]()
After students get a grip on adding matrices, you can move on to teaching subtracting matrices. Remind students that we use the same process as in matrix addition, that is, we’re only subtracting entries in matching positions. Illustrate this with an example, such as:
Subtract these two matrices:
![]()
![]()
By subtracting only the numbers in the corresponding positions, we’ll get:
8 – 2 = 6 4 – (-6) = 10
3 – (-7) = 10 0 – 2 = -2
Now we’ll simply write the four differences in the corresponding order in brackets, that is:
![]()
Point out that to add or subtract matrices, the matrices must have the same dimensions. For instance, a matrix with two rows and three columns can be added to another matrix with two rows and three columns, but it can’t be added to a matrix with three rows and three columns.
Provide a few examples of matrices with the same dimensions and matrices with different dimensions and ask students which matrices can be added or subtracted and which ones can’t.

Scalar Multiplication and Division
Explain to students that scalar multiplication or scalar division means multiplying or dividing a matrix with a real number (a scalar). You can then explain that in scalar multiplication or division, we’re simply multiplying or dividing each number in the matrix with the scalar.
Illustrate this with an example, such as the following:
![]()
How can we find 3A?
Point out that since we know that we must multiply each entry in the matrix A by 3, we’ll multiply each of the four numbers (-2), 0, 7, and 2 by 3.
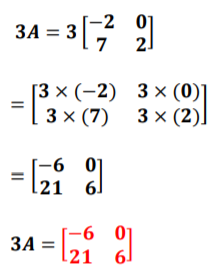
Tell students that we apply the same principle for division. However, things get a bit tricky if we want to multiply a matrix by another matrix, also known as matrix multiplication. At this point, it suffices to mention that that process is slightly different and you can leave matrix multiplication for the next classes in order not to overwhelm students.
Use this Guided Notes Worksheet (Members Only) to deepen children’s understanding of matrices and matrix operations. It contains both easy and more complex examples and operations, such as 3A – 2B. Print it out and hand out one worksheet per student.
This video is also a fun way to show students how we can use matrices in real-world situations, such as a CEO trying to predict how well their company will do in the next months based on the data on products that customers bought in the previous months. As this data is presented in matrix form, students can easily visualize the practical applications of matrices!
Activities to Practice Matrix Operations
Pair Work
Divide students into pairs and distribute this Assignment Worksheet (Members Only) to each student. The worksheet contains several math problems related to matrices and matrix operations, such as determining the dimensions of a given matrix or performing scalar multiplication.
Each student works individually and tries to solve the math problems. Once both students are done, they show their work to the other student they’re paired with and compare their results. It’s important that each student also shares how they reached a certain result.
The advantages of this kind of pair work are that struggling students can be paired up with students with a better grip on matrices, and can thus benefit from interpersonal learning. Just make sure you don’t end up pairing struggling with struggling students, as that can be ineffective.
Online Matrix Activity
Use these online exercises by Khan Academy to practice adding and subtracting matrices. Children play individually, so this activity is also great for parents who are homeschooling their children.
After children finish these math problems, continue with matrix equations for addition and subtraction where students have to find the x. That is, instead of being given two matrices to add or subtract, children get an equation where they have to find the missing matrix by using the difference or the sum. For instance:

Source: Khan Academy works
Finally, move on to these online exercises to practice scalar multiplication, and then scalar multiplication equations.
Before You Leave…
If you enjoyed this article on matrix operations, and you’re looking for more math materials for kids of all ages, sign up for our emails to receive loads of free content!
You can also head over to our blog – you’re guaranteed to find plenty of math resources that will help you best prepare for success in your lessons! And if you’re ready to sign up for membership, join us in the MathTeacherCoach community!
This lesson is based on:
Unit 0 – Preparing for Pre-Calculus



