Properties of Logarithms

Would You Rather Listen to the Lesson?

When pre-calculus students learn about logarithmic functions, one of the most important lessons they come across is the properties of logarithms. This is because students can simplify and evaluate logarithms with the help of these properties.

Even though log lessons may be challenging, math teachers can help make them more engaging and accessible by using various teaching strategies. We share a few such strategies in this article. Read on and learn more!

Strategies for Teaching Properties of Logarithms

Review Logarithms

Start your lesson on the properties of logarithms by briefly reviewing what logarithms are. Remind students that a logarithm is an exponent. That is, log_ax (“log base a of x”) is the exponent to which a must be raised to get x. You can present this in the following manner:

Where a > 0, a ≠ 1, and x > 0.

So logarithms are the opposite of exponentials, as they basically “undo” exponentials. You can also play this video in your class. The video introduces what logarithms represent, by using examples.

Then, check if there are any gaps in what students have learned so far on logarithms. For example, write a simple log on the whiteboard, such as log₂16 = x, and ask students to transform it into an exponent. Can most students easily say that the equivalent exponent is 2^x = 16?

What about evaluating logarithms? Have students acquired proficiency in evaluating a given log? For instance, write log₃81 = x on the whiteboard. Can students easily determine what this evaluates to, that is, log₃81 = 4? Practice a bit more and address potential gaps.

For more advanced practice examples on evaluating logarithms, use this brief online activity by Khan Academy. If you require detailed guidelines on teaching logarithms, as well as fun activities to practice logarithms, feel free to check out this article.

Properties of Logarithms

Now that you’ve briefly reviewed them, you can proceed with explaining the properties of logarithms. For starters, highlight that we use the properties of logarithms for simplifying and evaluating logarithms.

Add that with the help of these properties, we can rewrite logarithmic expressions, that is, we can expand or condense them. Point out that you will look into three such properties in this class, including:

multiplication property of logarithms
division property of logarithms
power rule of logarithms

Multiplication Property of Logarithms

Explain to students that the multiplication property of logarithms states that the logarithm of the product of two numbers is equal to the sum of individual logarithms of each number. Present this property on the whiteboard in the following way:

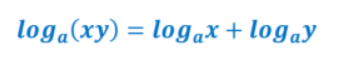
Division Property of Logarithms

Point out that according to the division property of logarithms, the logarithm of the quotient of two numbers is equal to the difference of the individual logarithm of each number. Present this property on the whiteboard in the following way:

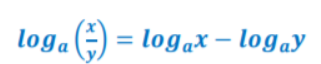
Power Rule of Logarithms

Finally, explain that the power rule of logarithms states that the logarithm of a number raised to a certain power is equal to the product of power and logarithm of the number. Present this property on the whiteboard in the following way:

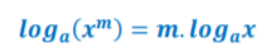
Example 1:

log₂8 + log₂32 = log₂(8 × 32)

log₂8 + log₂32 = log₂256

To check if this is correct, we can evaluate the logarithms, that is:

log₂8 = 3, because 2³ = 8

log₂32 = 5, because 2⁵ = 32

log₂256 = 8, because 2⁸ = 256

If we simply replace these values above in the statement log₂8 + log₂32 = log₂256, we’ll get the following:

3 + 5 = 8

So there you have it! We see that the multiplication property is true.

Example 2:

Additional Resources:

If you have the technical possibilities, you can also complement your lesson with multimedia material, such as videos. For example, use this video by Khan Academy to introduce the multiplication, as well as the division property of logarithms.

Afterward, play this video by Khan Academy to illustrate the power rule of logarithms. By rewriting and simplifying log5(x3) as 3log5(x), the video demonstrates how the logarithmic power rule applies.

Activities to Practice Properties of Logarithms

Properties of Logarithms Game

This is a simple online game that helps students sharpen their skills of simplifying and evaluating logarithms with the help of the properties of logarithms. To implement this game in your classroom, make sure that there is a sufficient number of devices for all students.

Students play the game individually, which makes the game suitable for parents who are homeschooling their kids, as well. Students are presented with different tasks, such as being asked to rewrite a log in a certain form by applying the properties of logarithms.

If they get stuck, students can also decide to play a video for help or use a hint. In the end, open space for discussion and reflection. Was any example particularly challenging? Why? Which properties did students use in their exercises?

Log Race

This is a fun game that will help students improve their knowledge of logarithms and properties of logarithms. To play this game in your class, you’ll need to print out this free Log Race Worksheet, some dice, chips and scissors, markers, and some paper.

Print out as many copies as needed depending on the size of your class. Cut out the task cards from the worksheet and separate them into different piles, depending on what is required in them. For instance, the cards where students should expand a log go into a ‘log’ pile.

Then, draw a game board shaped like a road with designated spaces (squares), as shown on the worksheet, with a ‘start’ and ‘finish’ space. Each space (or square) on the road has a specific instruction, such as ‘expand’, ‘rewrite as exponent’, ‘evaluate’ etc.

Launch the Game!

Divide students into groups of 3, with one person as a ‘checker’. Player 1 rolls the dice and moves their chip on the game board the number of spaces that they got with the dice (ex: if they got a 3 by rolling the dice, they move their chip three spaces on the game board.

The space the student lands on with their chip indicates what kind of a card the student should take. For example, if the student landed on a space that says ‘condense’, they need to draw the top card from the ‘condense’ pile and condense the logarithmic expression written on the card.

Each student has a few minutes to solve the task on their card. If they solve it correctly, they get to roll the dice and move again. If they solve it incorrectly, they lose their turn in the next round. The designated checker in each group checks the answers and keeps track of the scores.

As the name of the game indicates, the goal is to be the first one to reach the ‘finish’ space. If no one manages to reach ‘finish’ by the end of the class, the winner is the player that was closest to ‘finish’.

Before You Leave…

If you enjoyed these tips and activities for teaching properties of logarithms, you may want to check out our lesson that’s dedicated to this topic. So if you need guidance to structure your class and teach pre-calculus, make sure to sign up for more free resources here!

Feel free to also check out our article with free resources on properties of logarithms!

You can also sign up for our membership on MathTeacherCoach or head over to our blog – you’ll find plenty of awesome resources for kids of all ages!

This article is based on:

Unit 3 – Exponential and Logarithmic Functions