|
Would You Rather Listen to the Lesson?
|
When students start with precalculus lessons, they learn how to graph quadratic functions and what the properties of quadratic graphs are. They also develop an understanding of quadratic equations and learn about the different ways of solving them.
While entering the realm of pre-calculus may come across as scary for many students, there are many things that math teachers can do to support their students. To help put, we’ve compiled a list of guidelines for teaching quadratic functions and equations.
By following these guidelines, you’ll be sure to prepare your students for success in precalculus!

Quadratic Functions and Equations Definition
To begin with, you can explain what quadratic functions are. A quadratic function, also called a quadratic polynomial, is a function of the following form: f(x) = ax² + bx + c, where a, b and c are numbers and a is not a zero.
Provide an example, such as: f(x) = – 4x² + 10x + 9
Explain that in this case, a = – 4; b = 10 and c = 9.
Point out that there are cases where this is not so obvious, such as:
y = x²
Explain that this is also a quadratic function, in which a = 1; b = 0; and c = 0.
Finally, explain that a quadratic equation is simply an equation that has the following form:
ax² + bx + c = 0
Graphing Quadratic Functions
After defining them, explain how we graph quadratic functions. Point out that the graph of a quadratic function is a parabola that has a U form. Now demonstrate this with an example. Start with a simple quadratic function, such as:
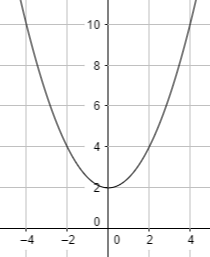
y = ½ x² + 2
Explain that when we’re unsure how to graph a function, we can start by replacing any value we want for x and then use the equation to solve for y. Then, we’ll plot the coordinates (x, y). We’ll do this by making a table of x and y values. This is the table method or:
| x | y = ½ x² + 2 | (x, y) |
| 2 | y = ½ 2² + 2 = 4 | (2, 4) |
| – 2 | y = ½ (- 2) ² + 2 = 4 | (- 2, 4) |
| – 4 | y = ½ (- 4)² + 2 = 10 | ( -4, 10) |
| 4 | y = ½ 4² + 2 = 10 | (4, 10) |
In other words, we’ll get the following parabole:
Quadratic Graphs Properties
Explain to students that quadratic graphs have specific properties, such as an axis of symmetry, a vertex of the parabola, a minimum and maximum. Use this video about quadratic functions to provide a visual illustration of these properties.
You can explain that an axis of symmetry of a parabola is a vertical line that divides the parabola into equal parts that mirror each other. The axis of symmetry formula is as follows:
![]()
Then, explain that the vertex of the parabola is simply the point where the parabola intersects its axis of symmetry. Introduce the formula for the coordinates of the vertex:
![]()
Point out to students that we can know whether a vertex is the lowest or the highest point on the graph, according to the coefficient a in front of x2 in the given quadratic function, that is, in f(x) = ax² + bx + c.
In other words, if the coefficient of x2 is negative, then the vertex will represent the lowest point on the graph. On the other hand, if the coefficient is positive, the vertex will represent the highest point on the graph.
Provide an example where the coefficient is negative and positive and ask students if they can tell whether the vertex will represent the highest or lowest point on the graph by looking at the coefficient. For example:
- y = – 4x² + 10x + 9
- y = x² + 10x
Point out to students that a quadratic equation can therefore have a minimum or a maximum. A maximum is the point where the graph has the maximum value, that is, the coefficient < 0. In this case, the vertex represents the maximum.
A minimum, on the other hand, is the point where the graph has the minimum value, that is, > . In this case, the vertex of the parabola represents the minimum.
Provide examples from this Guided Notes Worksheet (Members Only) to further illustrate the axis of symmetry, the vertex, and the minimum and maximum of a quadratic equation.
Solving Quadratic Equations
Explain to students that we can solve quadratic equations in three different ways, including:
- Factorization
- Completing squares
- Quadratic formula
Hand out this Guided Notes Worksheet (Members Only) to students to present the factorization and completing squares methods. Explain that these are methods that can make equations simpler, but they can’t always be applied. Highlight that this is why we use the quadratic formula, that is:
![]()
Provide an example of solving a quadratic equation while applying the above formula, such as:
2x² + 5x – 4 = 0
Ask students what are the values for a, b and c. By now, they should probably be able to tell you that a = 1, b = 5, and c = – 4. By replacing these values in the formula, we’ll get:
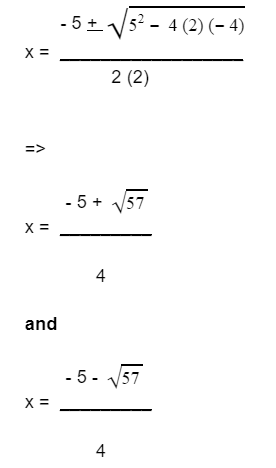
Quadratic Functions and Equations Quiz

Introduce this activity at the end of the unit, in order to review quadratic functions and equations. This is a simple quiz activity that doesn’t require a lot of preparation. Use the questions from these to worksheets: Assignment Worksheet (Members Only) and Exit Quiz Worksheet (Members Only) and insert them in PowerPoint slides.
Divide students into groups of four. Each group represents one team and is presented with a slide and a math question on the slide connected to quadratic functions and equations. For instance:
‘Solve this equation x² – 15x + 56 = 0 by using the quadratic formula’.
If a team answers correctly, they score a point. If they answer incorrectly, they lose 2 points. They can also use one ‘pass’ and decide to skip a question that they don’t know. In the end, the team that has the most points wins the game!
If you’re a homeschooling parent, you can adjust the worksheets into an individual game to play with your child.
Before You Leave…
If you liked our guidelines on teaching quadratic functions and equations above, you’ll also want to check out our whole lesson that goes in depth in this topic! For more guidance on how to structure your math lessons, make sure to sign up for our emails and get loads of free content!
And if you’re looking for more math materials for kids of all ages, sign up for a membership on MathTeacherCoach or head over to our blog – you’re guaranteed to find plenty of math resources that will greatly facilitate your work as a teacher.
This lesson is based on:
Unit 0 – Preparing for Pre-Calculus

