Teaching Functions in Precalculus

Would You Rather Listen to the Lesson?

In lessons on functions (precalculus), math students learn what function notation is and become proficient in evaluating and solving functions, including piecewise functions, as well as interpreting statements that use function notation in terms of a context.

Functions in precalculus may be challenging to grasp even for students who excel at math, and many math teachers may find themselves wondering how to better support their students. To lend a helping hand, we’ve created a list of tips that you can use in your classroom.

Without further ado, check out these awesome teaching tips and never let functions cause headaches for your students again!

How to Teach Functions (Precalculus)

Define Functions

Start by providing a definition of functions. A function is a relation that relates every element from one set with only one element from another set. As such, a function represents a relation where no two ordered pairs have the same first element.

It’s advisable to also point out that even though one element from one set (x) can’t relate to more than one element from another set (y); two or more elements from one set (x) can relate to the same element from another set (y).

You can illustrate a function on the whiteboard by drawing two such sets:

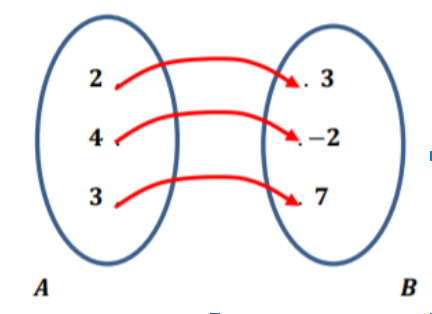
You can point out that since each element of set A has a unique output in set B, that is, each element from set A relates to exactly one element from set B, this drawing represents a function.

Function Notation

Add that function notation is a way to represent function with the help of symbols and signs. The most common function notation is f (x). We pronounce this as “f of x”. In this notation, x and f(x) refer to the domain and range of a function.

You may also want to check out our article on teaching relations and functions for Algebra 2, as well as this introductory video on functions.

Domain, Codomain, and Range

The set A of inputs is called the domain of the function. The set of all outputs is called range of the function, whereas the set B of all conceivable outputs is called the codomain of the function. So the domain is the set of values for x, whereas the range is the set of values for y.

Point out that there are several ways to write the domain of a function, including:

inequality notation, for example:

set-builder notation, for example:

Interval notation, for example:

You can also check out this video on the domain of a function, as well as this video on the range of a function.

Vertical Line Test

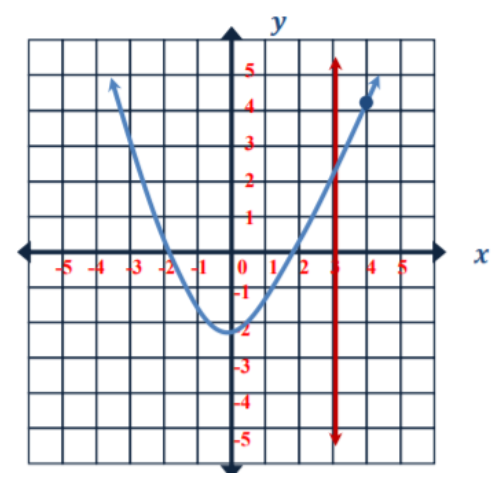
Explain to students that we can check whether a graph represents y as a function of x with the help of the vertical line test. Explain that the test is pretty straightforward – all we need to do is draw a vertical line that intersects the graph of a relation.

We then need to check the points of intersection – if the vertical line intersects the graph more than once, then the relation isn’t a function. A graph describes y as a function of x only and if only no two points lie on the same vertical line.

You can illustrate the vertical line test on the whiteboard. For instance, point out that this graph represents y as a function of x because we can draw a vertical line x = 3 that only intersects the graph once.

How to Evaluate and Solve a Function

Explain to students that evaluating and solving functions refers to the process of substituting the variable with a particular number. So when we know the input value and want to find out the output value, we say that we’re evaluating the function.

Present an example of evaluating and solving a function. For instance, evaluate this function:

f(x) = x² + 2x + 3

f(-2) = ?

Explain that we’ll take the input value, i.e. -2 and substitute the variable x:

f(-2) = (-2)² +2 (-2) + 3

f(-2) = 4 + (-4) + 3

f(-2) = 0 + 3

f(-2) = 3

You may also want to check out this video that contains more examples of evaluating functions.

Piecewise Functions

Explain to students that we can also create functions that act in a different way according to the different x values. We call these functions piecewise functions. They are functions in which there is more than one formula to define the output.

How do we evaluate piecewise functions? Provide an example of a piecewise function that needs to be evaluated, such as:

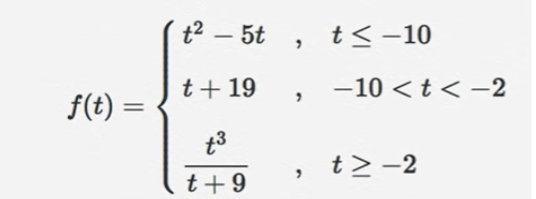
Credit: Khan Academy

Ask children to find the value of f(-10)? Explain that we can observe three formulas in this function, and the way to determine which formula we’ll use is by looking at which one fits best.

So we’ll try to find the case that fits this the best. In the first case, we can see that t is less than or equal to -10, and we know that t is going to be -10, since we’re asked to find the value of f(-10), we’ll use the top case: t² – 5t, t ≤ – 10.

We’ll use this case in that we substitute the variable t with -10:

f(-10) = (-10)²- 5(-10)

f(-10) = 100 + 50

f(-10) = 150

For more guidelines, you can also refer to this introductory video on piecewise functions, as well as this video that explains how to evaluate piecewise functions.

Activities to Practice Functions (Precalculus)

Exit Quiz

Use this game at the end of your lesson on functions. It will help students reinforce their knowledge of functions, such as evaluating and solving functions, including piecewise functions, as well as their knowledge of using the different types of function notation.

To prepare, you can create a PowerPoint with a different function question on each slide. You can use this Exit Quiz Worksheet (Members Only) for inspiration for creating the questions. Divide students into groups of 3 or 4 and provide instructions for the quiz.

Explain that each group is presented with a maths challenge related to functions and has a given number of minutes to solve the challenge. All members of the group work together to solve the challenge. If they manage to do so, they score 1 point. And if they don’t, they lose 1 point.

Groups take turns in answering the question that they were given. They don’t interfere in the challenges of the other groups. In the end, the group that has the biggest score wins the Exit Quiz game!

Before You Leave…

If you enjoyed these math strategies for teaching functions (precalculus), you should check out our lesson that’s dedicated to this topic. So if you need guidance to structure your class and teach pre-calculus, make sure to sign up for more free resources here!

You can also sign up for our membership MathTeacherCoach or head over to our blog – you’ll find plenty of awesome resources that are guaranteed to help you in your teaching!

This article is based on:

Unit 1 – Functions and Relations