Power and Radical Functions

Would You Rather Listen to the Lesson?

When learning about functions in precalculus, students familiarize themselves with what power and radical functions are, how to define and graph them, as well as how to solve equations that contain radicals.

Units in precalculus are often seen as challenging, and power and radical functions are no exception to this. To help out with your teaching, we’ve compiled a list of resources and teaching tips.

Without further ado, if you’re teaching power and radical functions, here are some great tips that you can apply to help you best prepare for success in your lessons!

How to Teach Power and Radical Functions

Power Functions

You can start your lesson on power and radical functions by defining power functions. Explain to students that power functions are functions of the following form:

In power functions, a represents a real number that’s not zero and n stands for any real number. Point out that a is also known as the coefficient. So power functions have a variable at their base (as we can see there’s the variable x in the base) that’s raised to a fixed power (n).

Before looking at the properties of power functions and their graphs, you can provide a few examples of power functions on the whiteboard, such as:

f(x) = – 5x²
f(x) = 2√x
f(x) = 3⁄x²
f(x) = 2x³

Point out to students that each function has a single term, and this is one way we can tell that these examples are power functions. The other condition is that the exponent is a real number. You can go through the exponents of each example and analyze them with the students.

Graphs of Power Functions

Explain that we can determine what the graph of a power function will look like based on a couple of things. In other words, we can determine one important property of power functions – their end behavior.

If n Is Even…

Highlight that we can predict the shape of the graph of a power function based on the value of n, and the coefficient a. For instance, if n is even and not a fraction, and n > 0, the left end behavior will match the right end behavior.

So the shape of the graph of the power function will look like this (for the power function y = x²):

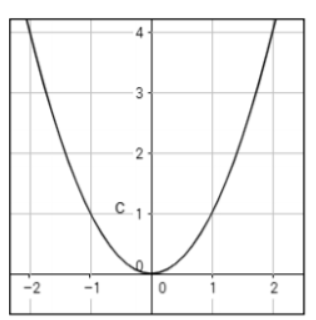
Point out that in the above case, we can see that there is a rise in both the left and right end behavior, which happens because n is even. Add that we also had a positive coefficient, that is, even though the coefficient is not visible, we can conclude there is a + 1 in front of x².

However, if we have the same power function but with a negative coefficient, y = – x², there will be a fall in the right end behavior, and if n is even, there will be a fall in the left end behavior as well. So the graph will look like this:

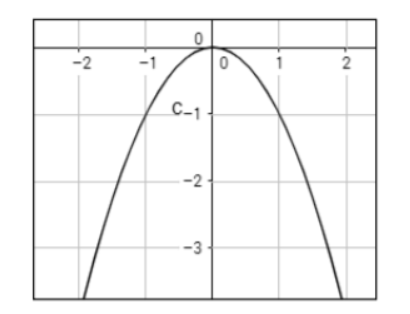
If n Is Odd…

On the other hand, in cases where n is odd, and not a fraction, and n > 0, the right end behavior won’t match the left end behavior. For instance, take the power function y = x³, where n is 3. Point out that the coefficient is + 1, that is, a positive number.

Remind students that from what we observed in the above cases where n was even, a positive coefficient indicates a rise in the right end behavior, which remains true even in cases where n is odd.

However, when n is odd, the left end behavior won’t match the right end behavior and we’ll witness a fall on the left end behavior. The shape of the graph of this power function y = x³ will look like this:

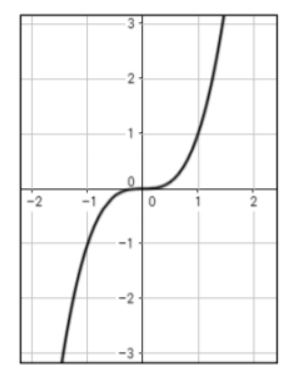
However, if we have the same power function but with a negative coefficient, in other words, y = -x³, we’ll have a fall in our right end behavior and the graph will look like this:

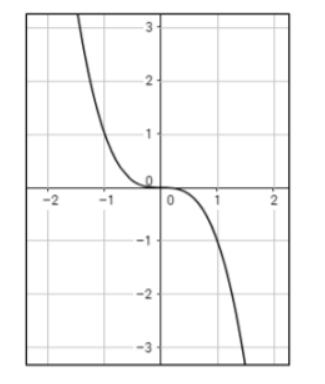
Radical Functions

Once you have explained power functions to students, you can move on to radical functions. Start by defining what a radical function is. You can simply state that a radical function is a function that can be written in this form:

Point out that a represents a real number, excluding zero, and n is any non-zero integer. So if a function is defined by a radical expression, we refer to it as a radical function. You can add that a square root function is f(x) = √x, whereas a cube function is f(x) = ³√x.

You can provide a few examples of power functions on the whiteboard, such as:

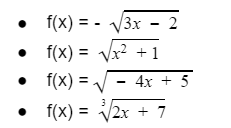
Graphs of Radical Functions

Point out that just like with graphs of power functions, we can determine the shapes of graphs of radical functions depending on the value of n in the given radical function. More specifically, what matters to us is whether n is even or odd.

When n is even, and it’s greater than zero, we have one side, half of the parabola or the positive range of this. For example, you can draw the graph of this simple radical function y = ²√x.

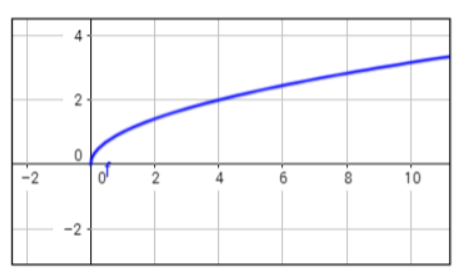
You can also present an example of what happens when the coefficient is negative, that is, if the function is y = – ²√x. The graph will look like this:

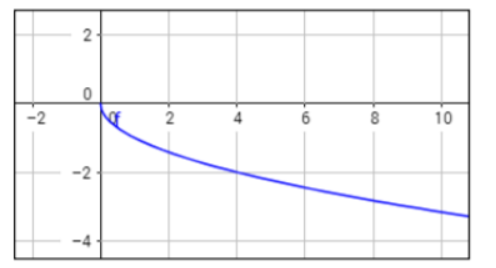
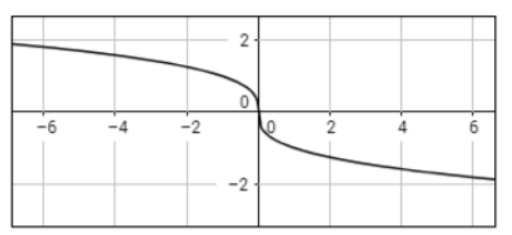
However, point out that when n is odd, we have a reflection of the graph on both sides. Provide an example of a radical function with an odd index n, and draw the graph on the whiteboard. For instance, by graphing the function y = ³√x, we will get the following:

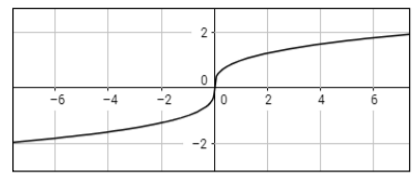
You can also provide an example of the same function when the coefficient is negative, that is, y = – ³√x, which will result in the following graph:

Solving Radical Equations

Explain to students that when solving radical equations, we isolate the radical expression on one side of the equation. Then, we raise the power on both sides of the equation (i.e. square both sides) to remove the radical signs.

In the end, we simplify the expression using algebra. Once we get the solutions, we check whether they are really the solutions. We substitute the values in the original equation and verify if it results in a true statement.

Example: Let’s say that we want to solve the following radical equation √2x – 2 = x – 1.

Since the first thing we want to do is isolate the radical expression, we can easily observe that the radical is already by itself on one side. This means that we can proceed with squaring both sides of the equation, which will result in the following:

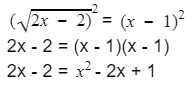
At this point, we can move all terms to the right side and factor out the trinomial:

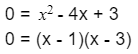
So our possible solutions are x = 1 and x = 3. However, we need to substitute these solutions in the original equation to verify this. By doing so, we can observe that true statements are produced, which means 1 and 3 are the true solutions.

Additional Resources:

If you have the technical means in your classroom, you can also choose to have a video lesson. Not only do students enjoy multimedia material, but complementing your lesson on power and radical functions with a video will be very practical when it comes to graphing the functions.

This video is a free resource with step-by-step explanations on what power and radical functions are, as well as how the shapes of their graphs can be determined depending on the n index, and depending on their coefficient.

In addition, you can use this free video for teaching how to solve radical equations. The video contains simple instructions and a worked-out example on how to solve square-root equations with two solutions.

Activities to Practice Power and Radical Functions

Online Graphs Game

This is a brief online game that will allow students to practice their knowledge of radical functions. To use this activity in your classroom, make sure there is a suitable technical device for each student.

This activity is played individually. Provide instructions to students. Explain that they will play a game where they are presented with several graphs of a given square or root function, and they have to identify which graph matches the exact function.

Pair Work

This is a simple activity that will help students practice graphing power and radical functions, as well as solving radical equations. As a bonus, the activity is also useful for reinforcing students’ peer tutoring skills. The only material needed is this Assignment Worksheet (Members Only).

Divide students into pairs and hand out the worksheets. Make sure there is one worksheet per student. Explain to students that they work individually to solve all the math questions in the worksheet.

Once they’re done, they exchange their sheets with the student that they’re paired with, and check the solutions. They should provide feedback and guidance to the student when necessary.

Before You Leave…

If you enjoyed these math tips for teaching power and radical functions, you should check out our lesson that’s dedicated to this topic. So if you need guidance to structure your class and teach pre-calculus, make sure to sign up for more free resources here!

You can also sign up for our membership MathTeacherCoach or head over to our blog – you’ll find plenty of awesome resources that are guaranteed to help you in your teaching!

This article is based on:
Unit 2 – Power, Polynomial, and Rational Functions