|
Would You Rather Listen to the Lesson?
|
When precalculus students learn about trigonometric functions on the unit circle, they learn how to understand the standard position of an angle, coterminal angle, and reference angle and become fluent in finding the trigonometric ratios in a given point on a unit circle.
Even though trigonometry can cause headaches for even the best of students, math teachers and homeschooling parents can facilitate the learning process by employing various teaching tips. To help out, we bring you a few such awesome tricks in this article.
Use them in your class and never worry about teaching this topic again!

Tips for Teaching Trigonometric Functions on the Unit Circle
What Is a Unit Circle?
For starters, you can explain to students that a unit circle is a circle whose radius is 1 unit. So the length from the center of the circle to any given point on the circle is of length 1. Provide a drawing to illustrate this:
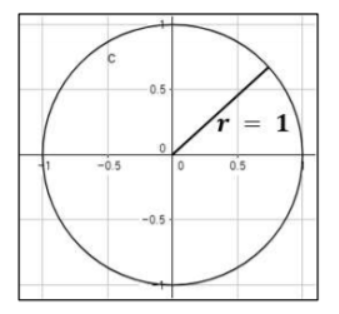
You could also complement your lesson with videos. For example, you could play this video as an introduction to what a unit circle represents. The video contains illustrations and explanations on how we can use a unit circle in math. This video is also a great resource.
Trigonometric Functions on a Unit Circle
Now that students understand what a unit circle is, you can proceed by explaining trigonometric functions on it. As students to consider a point P(x, y) on the unit circle with radius r = 1, making an angle with x-axis. Point out that we can write the six trigonometric ratios in this way:

Provide a drawing on the whiteboard illustrating this, such as the following drawing:
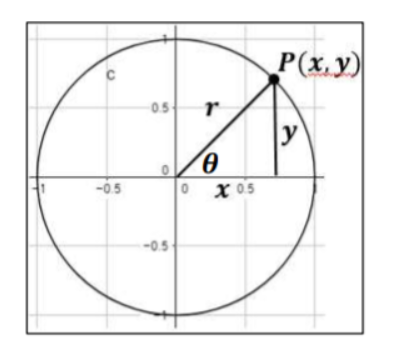
Standard Position
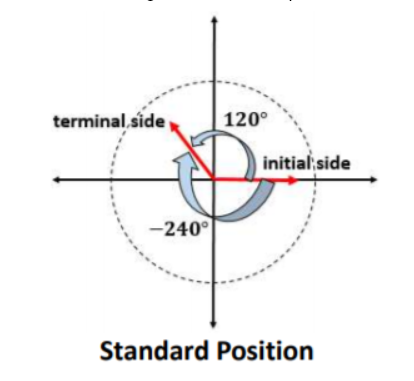
Explain to students that an angle is in standard position if its vertex is the origin and one ray is on the positive x-axis. We refer to the ray on the x-axis as the ‘initial side’. The other ray is called the ‘terminal side’.
Add that two angles that have the same terminal side are known as coterminal angles, whereas angles measuring 120° and −240° are called coterminal angles.
Provide a drawing of the standard position on the whiteboard:
Reference Angle

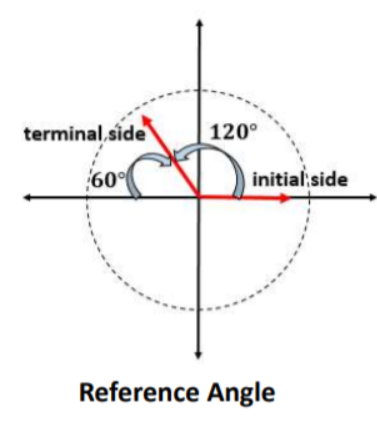
Explain to students that the acute angle that’s between the terminal side and x-axis is called a reference angle. Reference angles can appear in all four quadrants.
- If the starting angle is in the first quadrant, then the reference angle and the starting angle are the same
- If the starting angle is in the 2nd quadrant, then the reference angle is given by π – θ
- If the starting angle is in the 3rd quadrant, then the reference angle is given by θ − π
- If the starting angle is in the 4th quadrant, then the reference angle is given by 2π − θ
Provide a drawing on the whiteboard of a reference angle, such as the following:
Activities to Practice Trigonometric Functions on the Unit Circle
Group Work
This activity will help students practice trigonometric functions on the unit circle. To implement this activity in your classroom, the only thing you’ll need to do is print out this Assignment Worksheet (Members Only).
Divide students into groups of 3 or 4 and hand out the worksheets. Explain to students that the worksheets contain several exercises related to trigonometric functions on the unit circle, such as finding the reference angle for each given angle, etc.
Students work together with the other members of their group to complete the worksheets. Provide a few minutes for this. In the end, leave some time for discussion and reflection on the exercises. Ask students to explain which steps they took to solve the exercises.
Before You Leave…
If you enjoyed these tips on teaching trigonometric functions on the unit circle, you may want to check out our lesson that’s dedicated to this topic. So if you need guidance to structure your class and teach pre-calculus, make sure to sign up for more free resources here!
You can also sign up for our membership on MathTeacherCoach or head over to our blog – you’ll find plenty of awesome resources for kids of all ages!
This article is based on:
Unit 4 – Trigonometric Functions

